Just a few words about the Russian election. I read this entry http://www.badscience.net/2012/03/is-there-statistical-evidence-of-fraud-in-the-russian-election-data/ and thought to look for myself. For me it seems the data is not good enough to answer the fraud question.
Downloading data, reading and just look:
> r1 <- read.xls("xxxxxxxxxxxxxx")
> head(r1)
projecturl id updt region uik obstrusted INVALID VALID
1 http://sms.golos.org 1 38324.72 27 650 1 4 323
2 http://sms.golos.org 2 38689.09 25 216 0 9 927
3 http://sms.golos.org 3 38324.72 38 732 1 7 1282
4 http://sms.golos.org 4 38324.72 25 291 0 14 1185
5 http://sms.golos.org 5 38324.72 38 668 0 15 1510
6 http://sms.golos.org 6 38324.72 27 198 0 15 1889
Zhirinovsky Zyuganov Mironov Prokhorov Putin
1 42 40 3 24 214
2 88 229 58 92 460
3 80 333 46 150 673
4 129 315 67 175 499
5 76 395 70 227 742
6 127 353 115 379 915
Data looks good. Some unknown columns, region, VALID and the contenders look pretty straightforward.
Some regions occur once, others quite often. Some are completely missing
> regs <- xtabs(~ region,data=r1)
> names(regs[regs==1])
[1] "13" "32" "43" "65" "75" "86" "87"
Quite some difference in counts per region, as per the next plot. That is actually very odd, for someone not knowing about this field..
plot(xtabs(VALID ~ factor(region,levels=min(region):max(region)),data=r1))
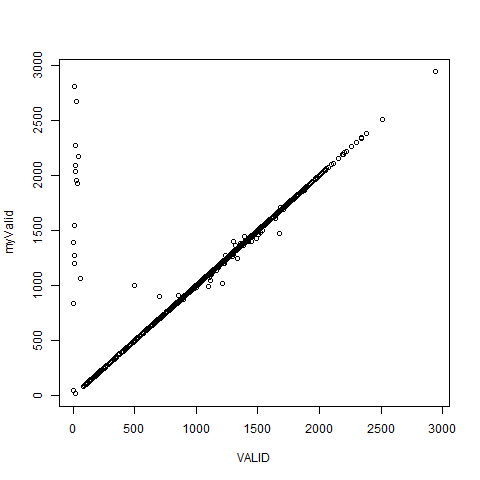
And, if we think VALID=Zhirinovsky + Zyuganov + Mironov + Prokhorov + Putin, that is not true either.
r1$myValid <- with(r1, Zhirinovsky + Zyuganov + Mironov + Prokhorov + Putin)
plot(myValid ~ VALID,data=r1)
The data just do not add together.
Conclusion
The data is either not complete and contains too many questions to even think about looking for fraud, or this is the true data and it is so bad as seen here and the fraud is obvious.
Tuesday, March 6, 2012
Sunday, March 4, 2012
Interpretation of R-index
Having introduced the R-index, it is time to look how it works. For this a simple example is sufficient. What happens if a product is different from another product. To make this at least slightly realistic, three products are needed. Two products will be equal, and one, the odd product, will have a varying distance. It is assumed, that the observations which a panelist does are normally distributed (sd=1) and based on these observations. Violating these assumptions is for a future time.
Again, critical values of R-indices are given by the red and blue lines (Bi and O'Mahony 1995 respectively 2007, Journal of Sensory Studies)
In the plot is is clear that R-index is more different from 50 as the odd product is more different from the others. At a distance of about 0.7 one has a fair chance to declare the odd product as different. At a distance 1.3 the odd product will almost certainly be declared different.
It is also clear that R-index is non-linear in terms of distance. With the current number of products and panelists, under 15 to 20 (or over 80 to 85) increasing the distance has less effect than closer to 50. R-index is therefore not a sensible distance measure.
The R code
library(plyr)
library(ggplot2)
makeRanksDiff <- function(prods,nrep) {
nprod <- length(prods)
inList <- lapply(1:nrep,function(x) rank(rnorm(n=nprod,mean=prods)))
data.frame(person=factor(rep(1:nrep,each=nprod)),
prod=factor(rep(1:nprod,times=nrep)),
rank=unlist(inList))
}
# R index for two products out of a cross table
tab2Rindex <- function(t1,t2) {
Rindex <- crossprod(rev(t1)[-1],cumsum(rev(t2[-1]))) + 0.5*crossprod(t1,t2)
100*Rindex/(sum(t1)*sum(t2))
}
# faster version - no labels
FastAllRindex <- function(rankExperiment) {
crst <- xtabs(~ prod + rank,data=rankExperiment)
nprod <- nlevels(rankExperiment$prod)
Rindices <- unlist( lapply(1:(nprod-1),function(p1) {
lapply((p1+1):nprod,function(p2) tab2Rindex(crst[p1,],crst[p2,])) }) )
Rindices
}
set.seed(12)
location <- seq(0,5,by=.1)
last <- lapply(location,function(xo) {
li <- lapply(1:250,function(xi) {
re <- makeRanksDiff(prod=c(0,xo,0),nrep=25)
FastAllRindex(re)
})
li2 <- as.data.frame(do.call(rbind,li))
li2$location <- xo
li2
} )
nprod <- 3
compare <- unlist(lapply(1:(nprod-1),function(p1) {
lap <- lapply((p1+1):nprod,function(p2) {
paste('Prod',p2,'vs','Prod',p1) })}) )
rankmatrix <- as.data.frame(do.call(rbind,last))
summy <- ddply(rankmatrix,~location,function(xo) {
what <- grep('location',names(xo) ,value=TRUE,invert=TRUE)
rb <- sapply(what,function(xi) quantile(xo[,xi],c(.025,.5,.975)))
rb <- as.data.frame(t(rb))
rb$what <- compare
rb
})
g1 <- ggplot(summy,aes(location,`50%`) )
g1 <- g1 + geom_point(aes(colour= what))
g1 <- g1+ geom_errorbar(aes(ymax = `97.5%`, ymin=`2.5%`,colour=what))
g1 <- g1 + scale_y_continuous(name='R-index' )
g1 <- g1 + scale_x_continuous(name='Location of odd product')
g1 <- g1 + geom_hline(yintercept=50 + 18.57*c(-1,1),colour='red')
g1 <- g1 + geom_hline(yintercept=50 + 15.21*c(-1,1),colour='blue')
g1
Again, critical values of R-indices are given by the red and blue lines (Bi and O'Mahony 1995 respectively 2007, Journal of Sensory Studies)
In the plot is is clear that R-index is more different from 50 as the odd product is more different from the others. At a distance of about 0.7 one has a fair chance to declare the odd product as different. At a distance 1.3 the odd product will almost certainly be declared different.
It is also clear that R-index is non-linear in terms of distance. With the current number of products and panelists, under 15 to 20 (or over 80 to 85) increasing the distance has less effect than closer to 50. R-index is therefore not a sensible distance measure.
The R code
library(plyr)
library(ggplot2)
makeRanksDiff <- function(prods,nrep) {
nprod <- length(prods)
inList <- lapply(1:nrep,function(x) rank(rnorm(n=nprod,mean=prods)))
data.frame(person=factor(rep(1:nrep,each=nprod)),
prod=factor(rep(1:nprod,times=nrep)),
rank=unlist(inList))
}
# R index for two products out of a cross table
tab2Rindex <- function(t1,t2) {
Rindex <- crossprod(rev(t1)[-1],cumsum(rev(t2[-1]))) + 0.5*crossprod(t1,t2)
100*Rindex/(sum(t1)*sum(t2))
}
# faster version - no labels
FastAllRindex <- function(rankExperiment) {
crst <- xtabs(~ prod + rank,data=rankExperiment)
nprod <- nlevels(rankExperiment$prod)
Rindices <- unlist( lapply(1:(nprod-1),function(p1) {
lapply((p1+1):nprod,function(p2) tab2Rindex(crst[p1,],crst[p2,])) }) )
Rindices
}
set.seed(12)
location <- seq(0,5,by=.1)
last <- lapply(location,function(xo) {
li <- lapply(1:250,function(xi) {
re <- makeRanksDiff(prod=c(0,xo,0),nrep=25)
FastAllRindex(re)
})
li2 <- as.data.frame(do.call(rbind,li))
li2$location <- xo
li2
} )
nprod <- 3
compare <- unlist(lapply(1:(nprod-1),function(p1) {
lap <- lapply((p1+1):nprod,function(p2) {
paste('Prod',p2,'vs','Prod',p1) })}) )
rankmatrix <- as.data.frame(do.call(rbind,last))
summy <- ddply(rankmatrix,~location,function(xo) {
what <- grep('location',names(xo) ,value=TRUE,invert=TRUE)
rb <- sapply(what,function(xi) quantile(xo[,xi],c(.025,.5,.975)))
rb <- as.data.frame(t(rb))
rb$what <- compare
rb
})
g1 <- ggplot(summy,aes(location,`50%`) )
g1 <- g1 + geom_point(aes(colour= what))
g1 <- g1+ geom_errorbar(aes(ymax = `97.5%`, ymin=`2.5%`,colour=what))
g1 <- g1 + scale_y_continuous(name='R-index' )
g1 <- g1 + scale_x_continuous(name='Location of odd product')
g1 <- g1 + geom_hline(yintercept=50 + 18.57*c(-1,1),colour='red')
g1 <- g1 + geom_hline(yintercept=50 + 15.21*c(-1,1),colour='blue')
g1
Friday, March 2, 2012
What is R-index
R index is developed in interpreting signal detection data for human perception. In sensory research it is used to interpret ranking data. The value one gets out of an R-index calculation is interpreted as a confusion between samples tested. It has been popularized among others by Bi and O'Mahony.
The value of R-index ranges between 0% and 100%, with 50% representing equality.
The computation of the R index is not difficult and can be done using a few short functions.
Simulated data of ranking for 3 persons and 4 products is:
person prod rank
1 1 1 1
2 1 2 3
3 1 3 2
4 1 4 4
5 2 1 1
6 2 2 4
7 2 3 3
8 2 4 2
9 3 1 1
10 3 2 4
11 3 3 3
12 3 4 2
These data has as R indices:
prod1 prod2 Rindex
1 1 2 100.00000
2 1 3 100.00000
3 1 4 100.00000
4 2 3 11.11111
5 2 4 22.22222
6 3 4 44.44444
It is not obvious at first sight, but the R index is in all actuality not a continuous function. There are only so many permutations of rankings. To demonstrate this, we repeat a simulation 1000 times. With 25 simulated persons with each 4 products the frequency of R-indices is shown in the figure.
It is clear that R index exactly 50% is the most probable outcome. This represents that the products are all equal. It is also clear that some R-indices which are really close to 50 are much less probable. Finally, values under 20 and over 80 hardly occur. This is well know. Critical values of R-indices are given by the red and blue lines (Bi and O'Mahony 1995 respectively 2007, Journal of Sensory Studies)
R code for these results
# A simple Ranking
makeRanksNodiff <- function(nprod,nrep) {
inList <- lapply(1:nrep,function(x) sample(1:nprod,nprod) )
data.frame(person=factor(rep(1:nrep,each=nprod)),
prod=factor(rep(1:nprod,times=nrep)),
rank=unlist(inList))
}
# R index for two products out of a cross table
tab2Rindex <- function(t1,t2) {
Rindex <- crossprod(rev(t1)[-1],cumsum(rev(t2[-1]))) + 0.5*crossprod(t1,t2)
100*Rindex/(sum(t1)*sum(t2))
}
# R index for all products out of an experiment
allRindex <- function(rankExperiment) {
crst <- xtabs(~ prod + rank,data=rankExperiment)
nprod <- nlevels(rankExperiment$prod)
Rindices <- lapply(1:(nprod-1),function(p1) {
lap <- lapply((p1+1):nprod,function(p2) {
index <- tab2Rindex(crst[p1,],crst[p2,])
prod1 <- levels(rankExperiment$prod)[p1]
prod2 <- levels(rankExperiment$prod)[p2]
data.frame(prod1=prod1,prod2=prod2,Rindex=index)
})
return(do.call(rbind,lap))
})
do.call(rbind,Rindices)
}
# small data set
set.seed(12)
rankExperiment <- makeRanksNodiff(nprod=4,nrep=3)
rankExperiment
allRindex(rankExperiment)
# larger simulation
set.seed(12)
last <- lapply(1:1000,function(x) {
re <- makeRanksNodiff(nprod=4,nrep=25)
ar <- allRindex(re)
ar$Rindex
} )
rankmatrix <- do.call(rbind,last)
RindicesTable <- as.data.frame(table(rankmatrix))
RindicesTable$Rindex <- as.numeric(as.character(RindicesTable$rankmatrix))
library(ggplot2)
g1 <- ggplot(RindicesTable, aes( Rindex, Freq)) + geom_point(alpha=.5)
g1 <- g1 + geom_vline(xintercept=50 + 18.57*c(-1,1),colour='red')
g1 <- g1 + geom_vline(xintercept=50 + 15.21*c(-1,1),colour='blue')
g1
The value of R-index ranges between 0% and 100%, with 50% representing equality.
The computation of the R index is not difficult and can be done using a few short functions.
Simulated data of ranking for 3 persons and 4 products is:
person prod rank
1 1 1 1
2 1 2 3
3 1 3 2
4 1 4 4
5 2 1 1
6 2 2 4
7 2 3 3
8 2 4 2
9 3 1 1
10 3 2 4
11 3 3 3
12 3 4 2
These data has as R indices:
prod1 prod2 Rindex
1 1 2 100.00000
2 1 3 100.00000
3 1 4 100.00000
4 2 3 11.11111
5 2 4 22.22222
6 3 4 44.44444
It is not obvious at first sight, but the R index is in all actuality not a continuous function. There are only so many permutations of rankings. To demonstrate this, we repeat a simulation 1000 times. With 25 simulated persons with each 4 products the frequency of R-indices is shown in the figure.
It is clear that R index exactly 50% is the most probable outcome. This represents that the products are all equal. It is also clear that some R-indices which are really close to 50 are much less probable. Finally, values under 20 and over 80 hardly occur. This is well know. Critical values of R-indices are given by the red and blue lines (Bi and O'Mahony 1995 respectively 2007, Journal of Sensory Studies)
R code for these results
# A simple Ranking
makeRanksNodiff <- function(nprod,nrep) {
inList <- lapply(1:nrep,function(x) sample(1:nprod,nprod) )
data.frame(person=factor(rep(1:nrep,each=nprod)),
prod=factor(rep(1:nprod,times=nrep)),
rank=unlist(inList))
}
# R index for two products out of a cross table
tab2Rindex <- function(t1,t2) {
Rindex <- crossprod(rev(t1)[-1],cumsum(rev(t2[-1]))) + 0.5*crossprod(t1,t2)
100*Rindex/(sum(t1)*sum(t2))
}
# R index for all products out of an experiment
allRindex <- function(rankExperiment) {
crst <- xtabs(~ prod + rank,data=rankExperiment)
nprod <- nlevels(rankExperiment$prod)
Rindices <- lapply(1:(nprod-1),function(p1) {
lap <- lapply((p1+1):nprod,function(p2) {
index <- tab2Rindex(crst[p1,],crst[p2,])
prod1 <- levels(rankExperiment$prod)[p1]
prod2 <- levels(rankExperiment$prod)[p2]
data.frame(prod1=prod1,prod2=prod2,Rindex=index)
})
return(do.call(rbind,lap))
})
do.call(rbind,Rindices)
}
# small data set
set.seed(12)
rankExperiment <- makeRanksNodiff(nprod=4,nrep=3)
rankExperiment
allRindex(rankExperiment)
# larger simulation
set.seed(12)
last <- lapply(1:1000,function(x) {
re <- makeRanksNodiff(nprod=4,nrep=25)
ar <- allRindex(re)
ar$Rindex
} )
rankmatrix <- do.call(rbind,last)
RindicesTable <- as.data.frame(table(rankmatrix))
RindicesTable$Rindex <- as.numeric(as.character(RindicesTable$rankmatrix))
library(ggplot2)
g1 <- ggplot(RindicesTable, aes( Rindex, Freq)) + geom_point(alpha=.5)
g1 <- g1 + geom_vline(xintercept=50 + 18.57*c(-1,1),colour='red')
g1 <- g1 + geom_vline(xintercept=50 + 15.21*c(-1,1),colour='blue')
g1
Subscribe to:
Posts (Atom)