In this post I want to analyze a first order pharmocokinetcs problem: the data of study problem 9, chapter 3 of Rowland and Tozer (Clinical pharmacokinetics and pharmacodynamics, 4th edition) with Jags. It is a surprising simple set of data, but still there is enough to play around with.
Data, model and analysis
The data is simple enough. One subject's concentration of cocaine (
μg/L) in plasma as function of time, after a starting dose of 33 mg cocaine hydrochlorine. The model is simple enough,
C=C0*exp(-k*t). A number of additional parameters are to be calculated, half-live (t1/2), Clearance (CL) and distribution volume (V). Additional information needed; molecular weight of cocaine 303 g/mol, cocaine hydrochloride 330 g/mol.
ch3sp9 <- data.frame(
time=c(0.16,0.5,1,1.5,2,2.5,3),
conc=c(170,122,74,45,28,17,10))
Bayesian model
This model has as feature that the (non-informative) priors are directly on the parameters which are in PK analysis important; distribution volume and clearance.
library(R2jags)
datain <- as.list(ch3sp9)
datain$n <- nrow(ch3sp9)
datain$dose <- 33*1000*303/340 # in ug cocaine
model1 <- function() {
for (i in 1:n) {
pred[i] <- c0*(exp(-k*time[i]))
conc[i] ~ dnorm(pred[i],tau)
}
tau <- 1/pow(sigma,2)
sigma ~ dunif(0,100)
c0 <- dose/V
V ~ dlnorm(2,.01)
k <- CL/V
CL ~ dlnorm(1,.01)
AUC <- dose/CL
t0_5 <- log(2)/k
}
parameters <- c('k','AUC','CL','V','t0_5')
inits <- function()
list(V=rlnorm(1,1,.1),CL=rlnorm(1,1,.1),sigma=rlnorm(1,1,.1))
jagsfit <- jags(datain, model=model1,
inits=inits, parameters=parameters,progress.bar="gui",
n.chains=4,n.iter=14000,n.burnin=5000,n.thin=2)
jagsfit
Inference for Bugs model at "...", fit using jags,
4 chains, each with 14000 iterations (first 5000 discarded), n.thin = 2
n.sims = 18000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
AUC 201.756 0.766 200.258 201.369 201.749 202.143 203.233 1.001 10000
CL 145.767 0.553 144.705 145.485 145.769 146.045 146.855 1.001 10000
V 147.568 0.496 146.607 147.320 147.569 147.819 148.515 1.002 18000
k 0.988 0.005 0.978 0.985 0.988 0.991 0.998 1.001 13000
t0_5 0.702 0.004 0.694 0.700 0.702 0.704 0.709 1.001 13000
deviance 6.769 4.166 2.236 3.801 5.682 8.557 17.538 1.001 6300
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 8.7 and DIC = 15.4
DIC is an estimate of expected predictive error (lower deviance is better).
The expected answers according to the book are:
AUC=0.200 mg-hr/L, CL 147 L/hr, V=147 L, t1/2=0.7 hr. The numbers are slightly off compared to the book, but the expectation is that students use graph paper and a ruler.
Alternative Baysian model
This is more or less the same model, however log(conc) rather than conc is modelled.
datain2 <- as.list(ch3sp9)
datain2$conc <- log(datain2$conc)
datain2$n <- nrow(ch3sp9)
datain2$dose <- 33*1000*303/340 # in ug cocaine
model2 <- function() {
for (i in 1:n) {
pred[i] <- c0-k*time[i]
conc[i] ~ dnorm(pred[i],tau)
}
tau <- 1/pow(sigma,2)
sigma ~ dunif(0,100)
c0 <- log(dose/V)
V ~ dlnorm(2,.01)
k <- CL/V
CL ~ dlnorm(1,.01)
AUC <- dose/CL
t0_5 <- log(2)/k
}
parameters <- c('k','AUC','CL','V','t0_5')
inits <- function()
list(V=rlnorm(1,1,.1),CL=rlnorm(1,1,.1),sigma=rlnorm(1,1,.1))
jagsfit2 <- jags(datain2, model=model2,
inits=inits, parameters=parameters,progress.bar="gui",
n.chains=4,n.iter=14000,n.burnin=5000,n.thin=2)
jagsfit2
Inference for Bugs model at "...93c1bb35a79.txt", fit using jags,
4 chains, each with 14000 iterations (first 5000 discarded), n.thin = 2
n.sims = 18000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
AUC 201.817 1.857 198.159 200.825 201.806 202.812 205.446 1.002 2700
CL 145.732 1.343 143.147 145.005 145.728 146.440 148.410 1.002 2700
V 146.904 2.248 142.588 145.702 146.882 148.049 151.428 1.002 2200
k 0.992 0.009 0.975 0.988 0.992 0.997 1.009 1.002 3200
t0_5 0.699 0.006 0.687 0.695 0.699 0.702 0.711 1.002 3200
deviance -37.541 3.922 -42.015 -40.424 -38.553 -35.772 -27.287 1.002 1900
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 7.7 and DIC = -29.9
DIC is an estimate of expected predictive error (lower deviance is better).
The results are fairly close to the first calculation, although the standard deviations are a bit larger. The question which is the better obviously depends on the expectations or knowledge on measurement error. The book states the data is adapted from a paper (
Chow et al., 1985, link to pdf), but that did not help me for this question.
Looking at residuals
I find classic regression to be a bit more convenient to help me with the structure of the error.
l1 <- lm(log(conc) ~ time,data=ch3sp9)
l1
Call:
lm(formula = log(conc) ~ time, data = ch3sp9)
Coefficients:
(Intercept) time
5.2994 -0.9922
n1 <- nls(conc~c0*(exp(-k*time)),
data=ch3sp9,
start=c(k=0.1,c0=120))
n1
Nonlinear regression model
model: conc ~ c0 * (exp(-k * time))
data: ch3sp9
k c0
0.9878 199.2918
residual sum-of-squares: 0.5369
Number of iterations to convergence: 5
Achieved convergence tolerance: 1.809e-07
par(mfrow=c(2,2))
plot(l1)
par(mfrow=c(1,1))
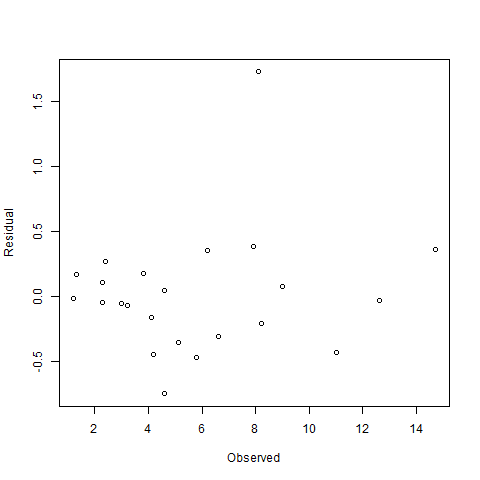
plot(x=predict(n1),y=resid(n1),main='nonlinear')
To me the non-linear model seems to have somewhat better behaving residuals.
Using a package
The package PKfit does offer these calculations. It is also completely menu operated, hence no code in this blog part. It does offer the possibility to specify error as shown here.
<< Weighting Schemes >>
1: equal weight
2: 1/Cp
3: 1/Cp^2
The results are in line with before.
<< Subject 1 >>
<< PK parameters obtained from Nelder-Mead Simplex algorithm >>
Parameter Value
1 kel 0.9883067
2 Vd 147.4714404
<< Residual sum-of-square (RSS) and final PK parameters with nls >>
0: 0.31284706: 0.988307 147.471
1: 0.31284252: 0.988292 147.474
2: 0.31284252: 0.988292 147.474
<< Output >>
Time Observed Calculated Wt. Residuals AUC AUMC
1 0.16 170 170.19433 -0.1943293 NA NA
2 0.50 122 121.53930 0.4607031 49.64 14.994
3 1.00 74 74.24673 -0.2467286 98.64 48.744
4 1.50 45 45.29682 -0.2968236 128.39 84.119
5 2.00 28 27.64910 0.3508985 146.64 114.994
6 2.50 17 16.87096 0.1290408 157.89 139.619
7 3.00 10 10.29481 -0.2948107 164.64 157.744
<< AUC (0 to infinity) computed by trapezoidal rule >>
[1] 174.7585
<< AUMC (0 to infinity) computed by trapezoidal rule >>
[1] 198.3377
<< Akaike's Information Criterion (AIC) >>
[1] 8.961411
<< Log likelihood >>
'log Lik.' -1.480706 (df=3)
<< Schwarz's Bayesian Criterion (SBC/BIC) >>
[1] 8.799142
Formula: conc ~ modfun1(time, kel, Vd)
Parameters:
Estimate Std. Error t value Pr(>|t|)
kel 9.883e-01 3.518e-03 280.9 1.09e-11 ***
Vd 1.475e+02 3.231e-01 456.4 9.58e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3537 on 5 degrees of freedom
Algorithm "port", convergence message: both X-convergence and relative convergence (5)
Conclusion: distribution of parameters
In hindsight the first Bayesian model is the one I prefer. Since I wanted to have some idea about the distribution of the parameters I have added this plot.
par(mfrow=c(3,2))
lapply(1:length(jagsfit$BUGSoutput$sims.list),
function(x) plot(density(jagsfit$BUGSoutput$sims.list[[x]]),
main=names(jagsfit$BUGSoutput$sims.list)[x]))