Data
Data exists in two data sets, training and test. The data are time series, each of a 1000 time points and some summary statistics of these. The training set consists of 63530 samples, the test set an additional 77769. In practice this means 490 Mb and 600 Mb of memory. Not surprising, just prepping the data and dropping it in randomForest gives an out of memory error. The question then is how to preserve memory.It seemed that my Windows 7 setup used more memory than my Suse 13.2 setup. The latter is quite fresh, while Win 7 has been used two years now, so there may be some useless crap which wants to be resident there. I did find that Chrome keeps part of itself resident, so switched that off (advanced setting). Other things which Win 7 has and Suse 13.2 misses are Google drive (it cannot be that hard to make it, but Google is dragging its heels) and a virus scanner, but there may be more.
This helped a bit, but this data gave me good reason to play a bit with dplyr's approach to store data in a database.
library(dplyr)
library(randomForest)
library(moments)
load('LATEST_0.2-TRAIN_SAMPLES-NEW_32_1000.saved')
my_db <- src_sqlite(path = tempfile(), create = TRUE)
#train_samples$class <- factor(train_samples$class)
train_samples$rowno <- 1:nrow(train_samples)
train <- copy_to(my_db,train_samples,indexes=list('rowno'))
rm(train_samples)
So, the code above reads the data and stores it in a SQLite database. At one point I made class a factor, but since SQLite does not have factors, this property is removed once the data is retrieved out of the database. I added a rowno variable. Some database engines have a function for row numbers, SQLite does not, and I need it to select records.
The key learning I got from this is related to the rowno variable. Once data is in the database, it just knows what is in the database and only understands its own flavour of SQL. Dplyr does a good job to make it as similar as possible to data.frames, but in the end one needs to have a basic understanding of SQL to get it to work.
Plot
The data has the property that part of it, the last n time points, are true samples. In this part the samples have an increase or decrease of 0.5%. The question is then what happens in the next part, further increase or decrease. The plot below shows the true samples of the first nine records. What is not obvious from the figure, is that the first two records have the same data, except for a different true part.First model
As a first step I tried a model with limited variables and only 10000 records. For this the x data has been compressed in two manners. From a time series perspective, where the ACF is used, and from trend perspective, where 10 points are used to capture general shape of the curves. The latter by using local regression (loess). Both these approaches are done on true data and all data. In addition, the summary variables provided in the data are used.The result, an OOB error rate of 44%. Actually, this was a lucky run, I have had runs with error rates over 50%. I did not bother to check predictive capability.
mysel <- filter(train,rowno<10000) %>%
select(.,-chart_length,-rowno) %>%
collect()
yy <- factor(mysel$class)
vars <- as.matrix(select(mysel,var.1:var.1000))
leftp <- select(mysel,true_length:high_frq_true_samples)
rm(mysel)
myacf <- function(datain) {
a1 <- acf(datain$y,plot=FALSE,lag.max=15)
a1$acf[c(2,6,11,16),1,1]
}
myint <- function(datain) {
ll <- loess(y ~x,data=datain)
predict(ll,data.frame(x=seq(0,1,length.out=10)))
}
la <- lapply(1:nrow(vars),function(i) {
allvar <- data.frame(x=seq(0,1,length.out=1000),y=vars[i,])
usevar <- data.frame(x=seq(0,1,length.out=leftp$true_length[i]),
y=allvar$y[(1001-leftp$true_length[i]):1000])
c(myacf(allvar),myacf(usevar),myint(allvar),myint(usevar))
})
rm(vars)
rightp <- do.call(rbind,la)
colnames(rightp) <- c(
paste('aacf',c(2,6,11,16),sep=''),
paste('uacf',c(2,6,11,16),sep=''),
paste('a',seq(1,10),sep=''),
paste('u',seq(1,10),sep=''))
xblok <- as.matrix(cbind(leftp,rightp))
rf1 <-randomForest(
x=xblok,
y=yy,
importance=TRUE)
rf1
Call:
randomForest(x = xblok, y = yy, importance = TRUE)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 6
OOB estimate of error rate: 44.21%
Confusion matrix:
0 1 class.error
0 2291 2496 0.5214122
1 1925 3287 0.3693400
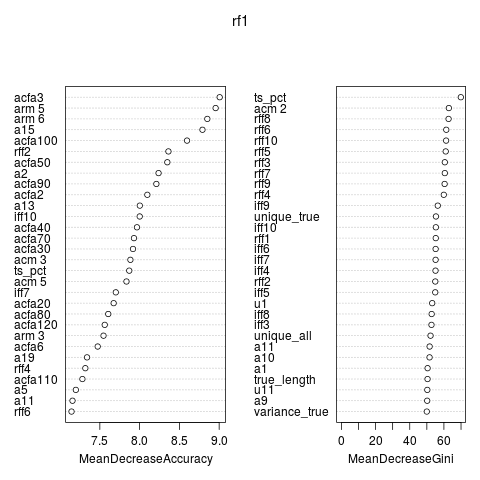
The plot shows the variable importance. Besides the variables provided the ACF seems important. Variables based on all time points seemed to work better than variables based on the true time series.
Second Model
In this model extra detail has been added to the all data variables. In addition extra momemnts of the data have been calculated. It did not help very much.mysel <- filter(train,rowno<10000) %>%
select(.,-chart_length,-rowno) %>%
collect()
yy <- factor(mysel$class)
vars <- as.matrix(select(mysel,var.1:var.1000))
leftp <- select(mysel,true_length:high_frq_true_samples)
rm(mysel)
myacf <- function(datain,cc,lags) {
a1 <- acf(datain$y,plot=FALSE,lag.max=max(lags)-1)
a1 <- a1$acf[lags,1,1]
names(a1) <- paste('acf',cc,lags,sep='')
a1
}
myint <- function(datain,cc) {
datain$y <- datain$y/mean(datain$y)
ll <- loess(y ~x,data=datain)
pp <- predict(ll,data.frame(x=seq(0,1,length.out=20)))
names(pp) <- paste(cc,1:20,sep='')
pp
}
la <- lapply(1:nrow(vars),function(i) {
allvar <- data.frame(x=seq(0,1,length.out=1000),y=vars[i,])
usevar <- data.frame(x=seq(0,1,length.out=leftp$true_length[i]),
y=allvar$y[(1001-leftp$true_length[i]):1000])
acm <- all.moments(allvar$y,central=TRUE,order.max=5)[-1]
names(acm) <- paste('acm',2:6)
arm <- all.moments(allvar$y/mean(allvar$y),
central=FALSE,order.max=5)[-1]
names(arm) <- paste('arm',2:6)
ucm <- all.moments(usevar$y,central=TRUE,order.max=5)[-1]
names(ucm) <- paste('ucm',2:6)
urm <- all.moments(usevar$y/mean(usevar$y),
central=FALSE,order.max=5)[-1]
names(urm) <- paste('urm',2:6)
ff <- fft(allvar$y[(1000-511):1000])[1:10]
ff[is.na(ff)] <- 0
rff <- Re(ff)
iff <- Im(ff)
names(rff) <- paste('rff',1:10,sep='')
names(iff) <- paste('iff',1:10,sep='')
c(myacf(allvar,'a',lags=c(2:10,seq(20,140,by=10))),
myint(allvar,'a'),
acm,
arm,
rff,
iff,
myacf(usevar,'u',seq(2,16,2)),
myint(usevar,'u')
)
})
#rm(vars)
rightp <- do.call(rbind,la)
xblok <- as.matrix(cbind(leftp,rightp))
rf1 <-randomForest(
x=xblok,
y=yy,
importance=TRUE,
nodesize=5)
rf1
Call:
randomForest(x = xblok, y = yy, importance = TRUE)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 10
OOB estimate of error rate: 42.76%
Confusion matrix:
0 1 class.error
0 2245 2542 0.5310215
1 1734 3478 0.3326938
SVM
Just to try something else than a randomForest. But I notice some overfitting.sv1 <- svm(x=xblok,
y=yy
)
sv1
Call:
svm.default(x = xblok, y = yy)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
gamma: 0.009259259
Number of Support Vectors: 9998
table(predict(sv1),yy)
yy
0 1
0 4776 2
1 11 5210
A test set (rowno>50000 in the training table) did much worse
ytest
0 1
0 547 580
1 6254 6149















